《编码》
前言
2022年初,逛B站时被某up主推荐的书,刚开始用ipad看电子版,越看越发现这本书的优质,电子版看着有点费眼并且不方便记笔记,因此在6月我购入了纸质书,7月中旬终于有空开始重新翻看一遍。
这本数非常适合想要了解计算机是怎么发明出来的,其中的原理以及电路组成是怎么回事的人,其中很多知识在大学的计算机组成原理,计算机导论以及微机原理等课程都有,没想到我会看得津津有味。
我有在考虑考研试试,读这本能够对整个计算机知识有个大致的了解,拿来热身下也是个不错的原则。
前五章
前五章主要通过一些有趣的生活故事开始,围绕两个小孩如果隔着房间通信的展开。从中引出了莫斯密码和简单的电路。
莫斯密码
莫斯密码由两种状态组成,可以是“滴”,“嗒”两种声音,也可以是“长亮”,“短亮”,甚至是其他的体现形式。而根据不同两种不同的状态组合可以对应不同的内容。
如下图,一个 ”短状态“和一个”长状态“组成字母A,一个”长状态“和三个”短状态“组成了字母B。

这里有个冷知识是:国际上的通用求救信号SOS的来源是其摩斯密码非常简单,即 ...---... ,易于记忆而被推广。
布莱叶盲文
最早的盲文是和普通文字一样,只是把文字换成浮雕那种样子,能够让盲人摸得到,这样看似符合直觉,却并没有帮助到盲人更加容易阅读。后来布莱叶发明了现如今的盲文系统。
布莱叶盲文 是由6个点构成,并且拥有着两种状态,凸起和平整,如下图所示,大黑点表示凸起,小黑点表示平整

如果你认真看上面的图你会发现,这25个英文字母(少了W)并没有用完这个盲文的所有组合,理论上,这个盲文能够显示 2的6次方个状态,也就是能够代表64种信息。
而布莱叶盲文确实发现了这个问题,于是布莱叶盲文能够表示数字,如下图

能够表示常用单词,如下图

还能表示音调,大小写,强调等等
布莱叶盲文中包括着优先码,换挡码,逃逸码等等,不难看出其已经颇具现代计算机编码的雏形。
而布莱叶盲文中最重要的,还是由6个点的2种状态表达不同信息这个概念。如果是8个点的2种状态,那么就能表达128种不同的信息,那如果是10个点,11个点呢?
懂行的看到这里,2进制这个概念已经呼之欲出了。
基础的电路
书中的第4章和第五章简单了讲了下初中物理,这里就不带大家复习了,有兴趣的自己光速看一下就了解了。
电报机与继电器
最早的电报是由人进行接力的,比方我要从两百公里外通过电路传输信息,那么中间需要几个人进行接力(早期的电路远距离传输是非常困难的),如下图,A传输到B,中间要经过A1,A2,A3的转发
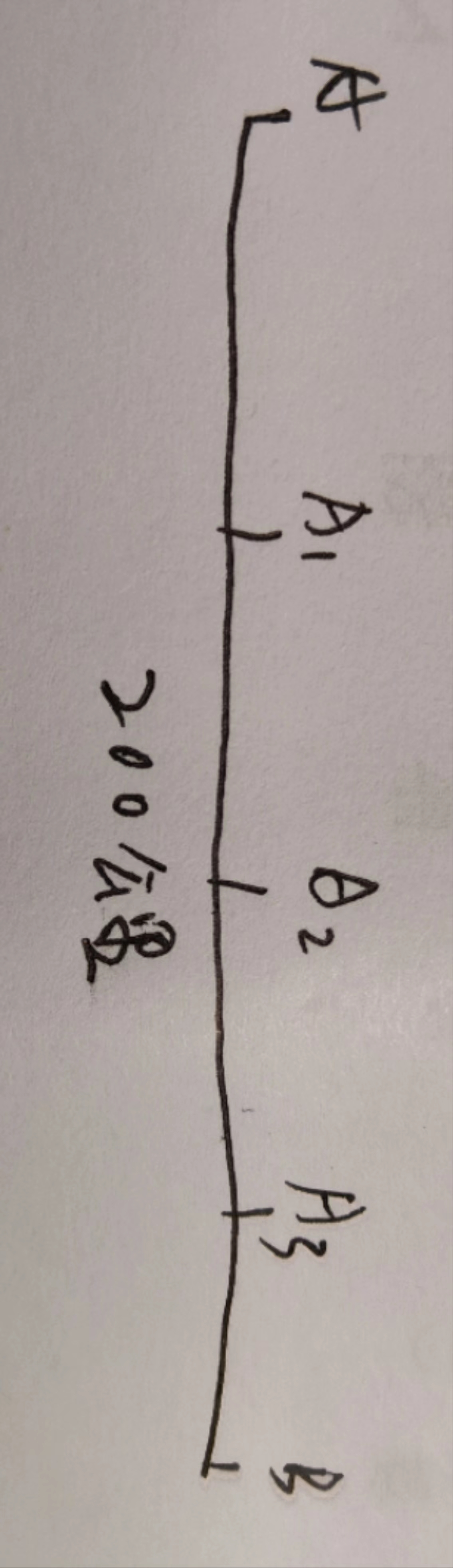
那么A1,A2,A3里的电报员工作,就是收听上一个传来的”嘀“,”嗒“电报声,并且原封不动的传给下一个。听起来就是个枯燥机械的工作。而后来,电磁感应的发现解决了这个无聊机械的工作。
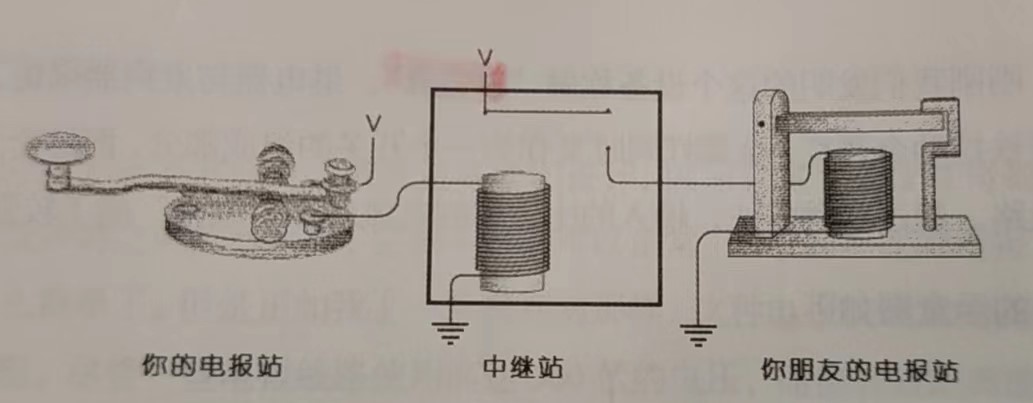
这里的中继站其实就是继电器,这是一�个非常重要的组件。
如上图,当你的电报站连通时,中继站的线圈会产生磁场把上面的开关拉下来,从而你朋友的电报站连通,线圈产生磁场把铁块吸下来。而当你电报站断开的时候,中继站的线圈失去磁场,开关恢复,你朋友的电报站断开线圈也失去磁场,铁块恢复,发出敲击声。
通过以上的过程,我们就可以实现在远程通过电报机让朋友的电报站发出 ”嘀“’,”嗒“两种状态的声音了。
不论距离多远,我们直接在中间加上继电器(中继站)就可以了。
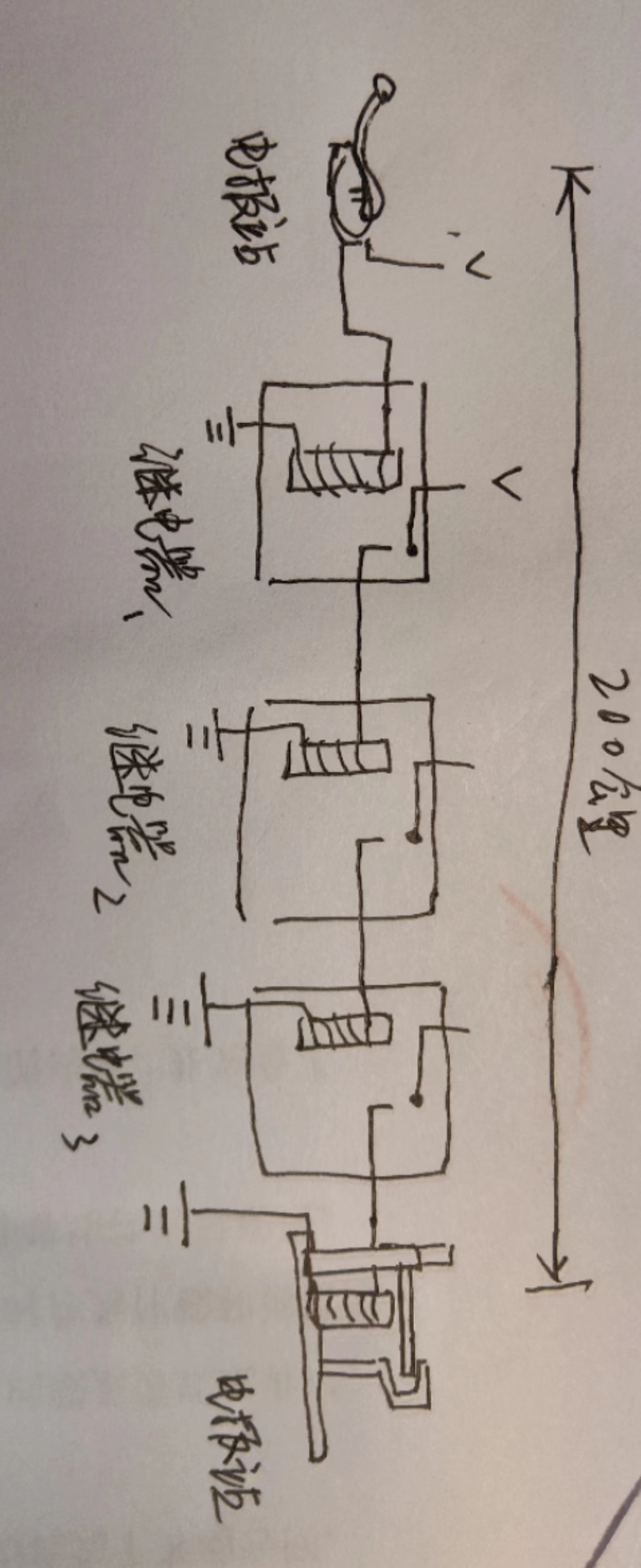
有了电磁感应,我们就可以去掉所有没有必要的人员,让电路自行运作了。而这就是迈向计算机的第一步。
我们的十个数字 与 十的替代品
作者提出了一个很有意思的想法,那就是之所以我们用十进制,是因为我们手指头一共有十个。
如果我们是卡通人物,那么我们手指头就是8个(如果你细心看动画片的话,角色手指头一般只有8个),那么我们数到8,就要进位了,因为手指头不够数下去了,那么卡通人物很可能就是采用8进制的数字系统。
如果我们是螃蟹,那么我们相当于有4个手指头,那么螃蟹如果演化出智慧,采用的就是4进制的数字系统。
如果��我们是海豚,只有两个鱼鳍,那么很明显就是采用2进制数字系统了。
那么不同进制之间的转化要怎么实现呢?只要记住数的量是不会变的就好了。
具体的换算篇幅我直接用公式表达:
即:N + aN^2 +bN^3 + cN^4 + dN^5 + eN^4 + fN^4 = M
M为转化前的数的量,N则是代表进制,如果是2进制,N就是2;如果是4进制,N就是4。
转化后的数就是 fedcbaN。
二进制数
这篇就是对之前的摩斯密码和布莱叶盲文的展开,将二进制数能够包含信息做了更深的讲解。
小知识点:1 bit = 一个二进制数
本章中花了大篇幅将了条形码的原理,条形码由两种形式构成,黑条和空白,正好对应了二进制中的0和1,一个条形码扫描出来是就是一堆二进制数

二进制数根据其相应的规则就能转化成对应的产品编号。
这一套规则能够让条形码从右往左和从左往右读都能准确地对应到同一个产品编号上。并且其中的模校验字符能过实现冗余了,保证条形码的安全性,非常有意思。
逻辑与开关
首先是介绍了布尔代数,这个和我们传统代数不一样,虽然用的符号一样。
关键知识点:布尔代数
布尔代数中:
-
基础:
- A + B 表示 A和B的并集,+ 可以用OR来表示,即 A OR B
- A x B 表示A和B的交集, x可以用AND来表示,即 A AND B
- 1 - N 表示非N, 1- 可以用NOT来表示,即NOT N
-
规则:
- 符合交换律,结合律,分配律,甚至是加法分配乘法也能成立:
加法分配乘法:W + (B X F) = (w + B) x (w + F)
- 等号的两边相等式子才成立
布尔代数和电路可以和电路很好的结合在一起。
并集(+/OR)可以用并联电路来表示,而交集(X/AND)可以用串联电路来表示。
文中举了一个很有意思的例子,